CMPS 260 Spring 2025
Homework #4: Regular Expressions, Regular Language Closure Properties
Due: 2pm, Monday April 7

Where r is a regular expression, L(r) denotes the language (i.e., set of strings) described by r. Where M is a finite automaton, L(M) denotes the language (i.e., set of strings) accepted by M.

1. Present a list containing precisely those strings of length five that are members of L( (ab + c)^*a ). Arrange the strings in alphabetical order.

2. Present a list containing precisely those strings of length five or less that are members of

Arrange the strings from shortest to longest; within each group of strings having the same length, put them in alphabetical order.

3. To the right is a four-state NFA, except with no final/accepting states identified. Let M_i (for i=0,1,2,3) be the NFA obtained by making q_i the lone final/accepting state.

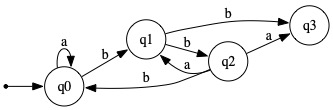
Present a regular expression describing ...

(a) L(M₀)     (b) L(M₁)     (c) L(M₂)     (d) L(M₃)

4. For each of the languages described below, present a regular expression that represents it. (Note: Zero is even.)

(a) {a^2kba^2m+1   |   k,m≥ 0 }
(b) Set of strings over {a,b} in which an even number of occurrences of a lie between every two occurrences of b.
(c) Set of strings over {a,b,c} in which an even number of occurrences of a lie between every two occurrences of b.
(d) Set of strings over {a,b} in which an odd number of occurrences of b lie between every two closest occurrences of a. (That is, in any substring of the form ab^ka, k is odd.)
(e) { w ∈ {a,b,c}^*   |   each of b and c occur in w exactly once }
(f) Set of strings over {a,b} in which aba does not occur as a substring.

5. For a language L, define CannotExtend(L) like this:

In words, CannotExtend(L) is that subset of L containing precisely those members of L that are not proper prefixes of any members of L. Another way to describe such strings is to say that they are the members of L that cannot be extended (via concatenation) to obtain longer members of L.

Describe a construction by which to obtain, from any DFA M, a new DFA M' such that L(M') = CannotExtend(L(M)). (You can assume that M is minimal.) This will demonstrate that regular languages are closed under the "cannot extend" operation.

6. For a language L ⊆ Σ^*, where $ ∉ Σ, define InsertOne$(L) like this:

In words, InsertOne$(L) contains precisely those strings that can be obtained by inserting one $ anywhere within any member of L (including at the beginning or end).

Describe a construction by which to obtain, from any NFA M, a new NFA M' such that L(M') = InsertOne$(L(M)). This will demonstrate that regular languages are closed under the "insert one $" operation.

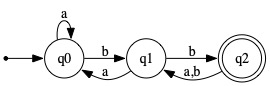
Apply your construction to the DFA shown to the right and show the result.

Hint: M' should have twice as many states as M. Indeed, let the state set of M be Q; then the state set of M' should be Q ∪ Q', where Q' = {q' | q ∈ Q}.

7. For a string x ∈ {a,b,c}^*, define ERASE*_a(x) to be the set of all strings obtainable from x by erasing zero or more occurrences of a. For example,

ERASE*a(baabcabacb)   =

{ baabcabacb,    babcabacb, baabcbacb, baabcabcb,    bbcabacb, babcbacb, babcabcb, baabcbcb,    bbcbacb, bbcabcb, babcbcb    bbcbcb }

Extending the definition to apply to languages, we have

That is, y ∈ ERASE*_a(L) iff y can be obtained by erasing zero or more occurrences of a from some x ∈ L.

Describe a construction by which to obtain, from any regular expression r, a new regular expression r' such that L(r') = ERASE*_a(L(r)). This will demonstrate that regular languages are closed under the "erase zero or more a's" operation.

As an example, show the regular expression resulting from applying your construction to the regular expression