Each of the first four problems describes a language and asks you to present an NFA —with a specified maximum number of states and/or transitions— that accepts that language. In counting states and transitions, you need not include the dead state or any transitions directed to it. Nor do you need to show that state or those transitions, as it is understood that if, in a transition graph, a state q has no outgoing transition on a symbol a, it is as though there were such a transition and it went to the dead state.
1.
Present an NFA having at most four states and seven transitions
that accepts the language
In words, L1 contains precisely those strings over the alphabet {a,b} having ab as a substring and a as a suffix.
Note that an edge in the transition graph that is labeled by both a and b counts as two transitions.
2. Present an NFA having at most six states and at most ten transitions that accepts the language
In words, L2 contains precisely those strings over the alphabet {a,b,c} in which, if c occurs, it occurs only as a suffix; if not, either bab is a suffix or baab is a substring.
Note that an edge in the transition graph labeled by multiple symbols counts as that number of transitions.
3. Present an NFA having at most seven states (only one final state is necessary) that accepts the language
In words, L3 contains precisely those strings over {a,b} that end either at least two symbols after an occurrence of aba or exactly one symbol after an occurrence of abb.
4. Present an NFA that accepts the language
The NFA should have only four states and only two transitions on each of the symbols a and b. λ-transitions are necessary.
An appropriate algorithm for removing λ-transitions is described in the section titled Step 1 in the web page that describes the Subset Construction algorithm (by which to obtain a DFA equivalent to a given NFA).
| Transition Graph | Table | ||||||
|---|---|---|---|---|---|---|---|
 |
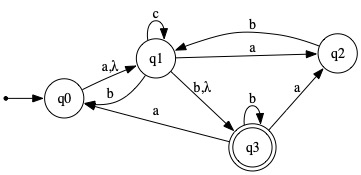
Init? | Final? | State | δ(_,a) | δ(_,b) | δ(_,c) | δ(_,λ) |
| ✓ | q0 | {q1} | ∅ | ∅ | {q1} | ||
| q1 | {q2} | {q0,q3} | {q1} | {q3} | |||
| q2 | ∅ | {q1} | ∅ | ∅ | |||
| ✓ | q3 | {q0,q2} | {q3} | ∅ | ∅ | ||
6. Present the DFA obtained by applying the Subset Construction algorithm to the NFA shown below. It should have seven states, including the dead state.
Present your answer in tabular form (as on the right side of the figure below) rather than as (or in addition to, if you want) a transition graph. Don't forget to identify the initial state and the final states.
Your DFA's state names should make obvious which subset of the NFA's state set each one corresponds to. For example, q{0,2} (or simply {0,2}, if you prefer) could be the name of the state corresponding to the set of states {q0, q2} in the given NFA.
| Transition Graph | Table | ||||
|---|---|---|---|---|---|
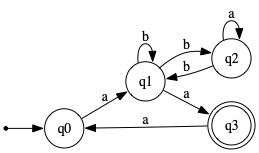 |
Init? | Final? | State | δ(_,a) | δ(_,b) |
| ✓ | q0 | {q1} | ∅ | ||
| q1 | {q3} | {q1q2} | |||
| q2 | {q2} | {q1} | |||
| ✓ | q3 | {q0} | ∅ | ||