CMPS 260: Example (Determinstic) Finite Automata
from page 61 of Lewis & Papadimitriou

Below left are five deterministic finite automata (DFAs) (taken from page 61 of the book by Lewis & Papadimitriou). To their right are remarks about the first two, followed by descriptions of the languages that they accept. (Please excuse the scribbles!)

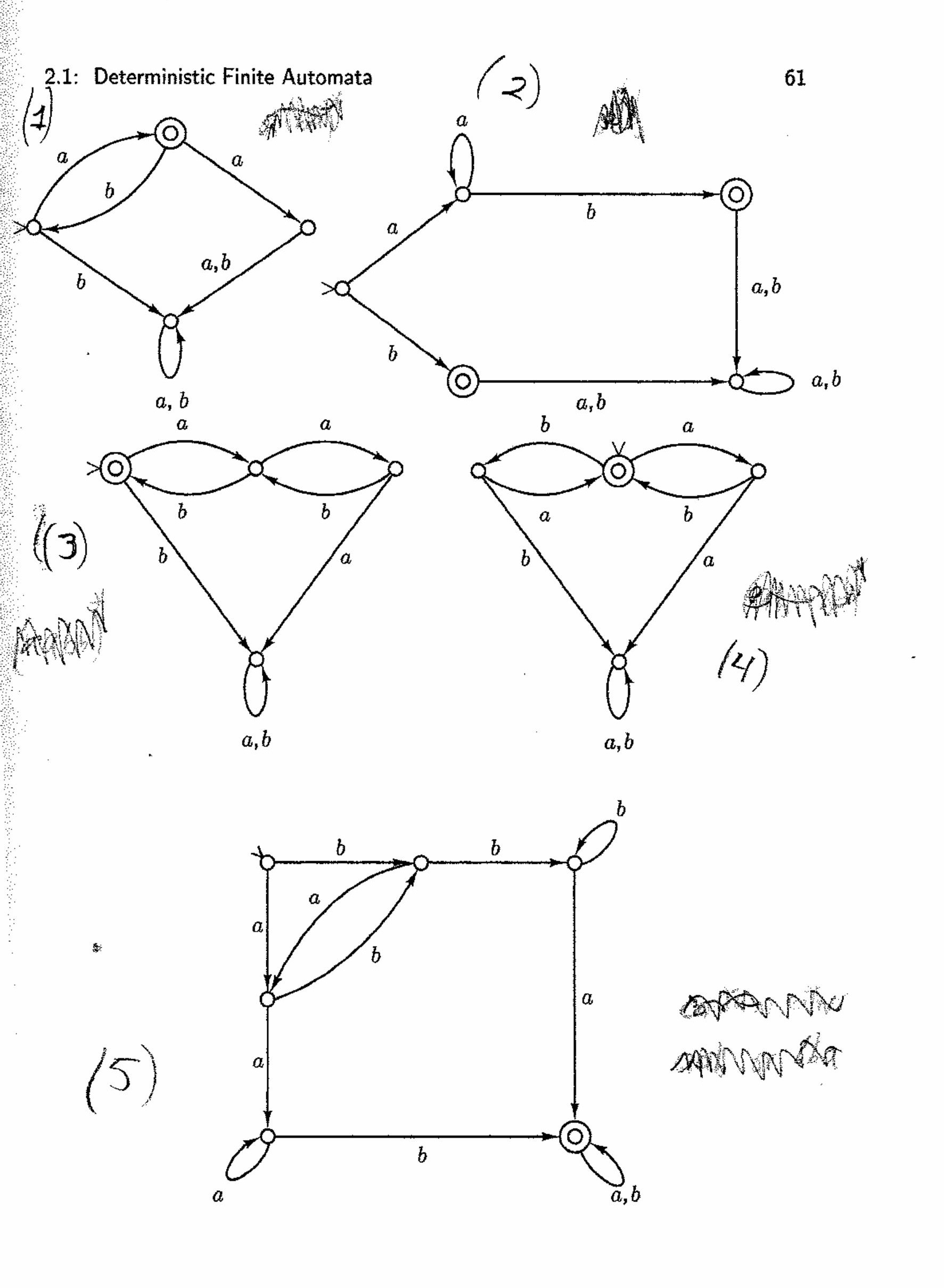
One could observe that neither DFA (1) nor (2) is minimal. In (1), the state reached from the initial state by the string aa is just as dead as the more obvious dead state, and thus those two states can be merged. In DFA (2), the two accepting states are indistinguishble and hence can be merged into a single state. For that matter, the initial state and the one it reaches via input a are also indistinguishable and thus can be merged. Doing both mergings results in a DFA having only three states, which is minimal for the language that it accepts.   set notation regular expression (1) { a(ba)n | n≥0 } a(ba)* (2) { anb | n≥0 } a*b (3) { (a(ab)mb)n | m,n≥0 } (a(ab)*b)* (4) { {ab, ba}n | n≥0 } (ab + ba)* (5) { xaaby | x,y ∈ {a,b}* } ∪ { xbbay | x,y ∈ {a,b}* } (a+b)*(aab + bba)(a+b)*

The set notation for DFAs (3) and (4) is not particularly good. In (3), it must be understood that there is no single value for m. That is, there is no requirement that for each of the n "iterations" of (a(ab)*b) the ab is repeated the same number of times. Hence, a more accurate set notation for this language would be