CMPS 260: Introduction to Finite State Machines by way of Mealy Machines

A computation involves inputs and outputs. Typically, we intend for there to be a specific relationship between those inputs and outputs. For example, if the intent is for the computation to perform an addition of two numbers provided as inputs, then we would not be satisfied if the output were not the number corresponding to their sum.

So think of a computer as a device, or "black box", that consumes inputs and produces outputs. Abstract away the details as to how the inputs are provided to it (e.g., button presses (such as via a keyboard or even buttons on the box itself) or mouse movements, or sensors) and in what form the output takes (e.g., textual, numbers, images, sounds). In simplest form, we can think of the inputs as being encoded as a string of bits (0's and 1's) and similarly the output. In fact, this is how things work on actual digital computers!

If you don't yet appreciate the power of using 0's and 1's to encode any kind of data, you should once you have gotten deeper into CMPS 250.

Let's consider a few simple computational problems whose solutions must realize a particular mapping between the bit strings provided as input and the outputs produced by the computation.

• Unary Count: The output string is to be a sequence of 1's of the same length as the input string. Example: 0110010 maps to 1111111.
  Such a machine must produce a reaction (i.e., emit an output) each time a stimulus is applied/presented to it (i.e., each time it reads/consumes an input symbol).
• Echo: The output string is to be identical to the input string. Example: 0110010 maps to 0110010.
  Such a machine must produce a reaction each time it reads/consumes an input symbol, and that reaction must depend upon the value of the input symbol. That is, it must be able to distinguish between different varieties of stimuli (here, 0 vs. 1).
• Complement: The output string is to be the "complement" of the input string (meaning that each bit is flipped). Example: 0110010 maps to 1001101.
• Unary Count of 0's: The output string is to be a sequence of 1's having length equal to the number of occurrences of 0 in the input string. Example: 0110010 maps to 1111.
  This is like Echo, except that the machine produces no (visible, at least) reaction to occurrences of 1's in the input string.
• Half-Length: The output string is to be a sequence of 1's of length equal to (the floor of) half the length of the input string. Example: 0110010 (of length seven) maps to 111 (of length three) because ⌊7/2⌋ = 3.

  Contrary to the previous problems, a machine solving this one cannot simply react (or refrain therefrom) to each input symbol as it is read, without regard to the string of input symbols that it has already read/consumed. Indeed, the machine must "remember" the parity (evenness vs. oddness) of the number of bits that it has read "so far".

• Bit-Flip Counter: The output string is to be a sequence of 1's having length equal 01 or 10. Example: 0110010 maps to 1111 (of length four) because 01 occurs twice, as does 10).

  A machine solving this problem must be such that its reaction to each input bit depends not only upon the value of that bit but also upon the immediately preceding input bit (if any). Thus, it needs to distinguish between the three situations "no bits have been read yet" vs. "the preceding bit was a 0" vs. "the preceding bit was a 1".

• Length-3-Run Reporter: The output string is to be a sequence of bits in which each occurrence of 0 (respectively, 1) corresponds to an occurrence of 000 (respectively, 111) in the input string, and in the same order. Example: 10000101110000101110111001 maps to 0010011 (Note that each occurrence of 0000 includes two (overlapping) occurrences of 000.)
  A machine that solves this problem must "remember" at least the two most recently read input bits.
• 01101-Occurrence Counter: The output string is to be a sequence of 1's having length equal to the number of occurrences, within the input string, of 01101. Example: 11011011010 maps to 11 (as there are two occurrences of 01101, which happen to overlap).
  A machine solving this problem must "remember", at a minimum, the longest bit string that is both a prefix of 01101 and a suffix of that portion of the input string read so far.

For the purpose of formalizing the notion of a machine "remembering" something about the current "situation" we use the concept of state. To formalize the notion of the situation changing as a result of a bit having been read, we use the concept of transition (i.e., from one state to another). A computation can be thought of as a discrete sequence of steps, where each step begins with the machine in some (current) state. A computation step involves the machine

1. reading an input symbol,
2. (possibly) producing some output, and
3. transitioning into some state (possibly remaining in the current state)

Which output is produced and to which state a transition occurs is a function of (i.e., is determined by) the current state and the value of the just-read input symbol.

It turns out that each of the problems described above can be solved by a machine having a finite number of states. Such a machine is called, naturally, a finite state machine (FSM) or a finite (state) automaton (FA). Most of our work in this course will involve FSMs that, in effect, produce only one bit of output, the value of which is interpreted as the answer to a YES/NO question. The variety of FSMs that solve the problems listed above are usually called Mealy machines. According to Wikipedia:

The Mealy machine is named after George H. Mealy, who presented the concept in a 1955 paper, "A Method for Synthesizing Sequential Circuits".

One way to describe an FSM is by using an edge-labeled directed graph, often called a transition graph. Each vertex/node corresponds to a state and each edge corresponds to a transition. Each edge is labeled by the input symbol that triggers it and the output that is produced when the transition is taken, separated by a slash.

Below are transition graphs describing single-state FSMs that solve the first four problems listed above.

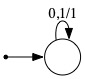
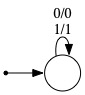
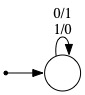
Unary count	Echo	Complement	Unary Count of 0's

For presentation purposes, in each transition graph the single edge really represents two different transitions, one for input 0 and the other for input 1. In the transition graph for Unary Count, the edge has label 0,1/1, which is shorthand for two edges, one labeled 0/1 and the other labeled 1/1. In the remaining transition graphs, the lone edge has two labels, which is shorthand for two edges, each having one of those labels. The Greek letter λ represents the empty string, which when appearing after the slash in an edge label means that no output is produced as a result of that transition being triggered.

Below are transition graphs describing FSMs that solve the last four problems listed above. In the last one, edge labels include output information only if a non-λ output is produced.

Half-Length	Bit-Flip Counter

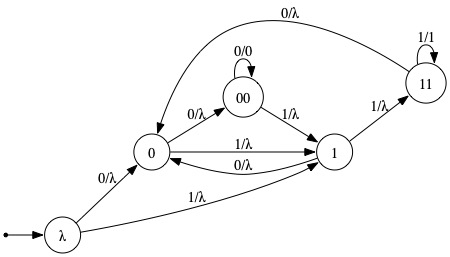Length-3-Run Reporter

01101-Counter