CMPS 260
Removing Useless Symbols from a Context-free Grammar

Background

A symbol (either nonterminal or terminal) appearing in a context-free grammar (CFG) is said to be useful if it appears in some sentential form in a derivation of a terminal string from the grammar's start symbol. That is, X is useful if there is a derivation of the form

S ⇒* αXβ ⇒* z

where S is the start symbol and z is a string of terminal symbols.

To be useful, a symbol must be both fruitful and reachable. X is fruitful if there is a derivation X ⇒* z, where z is a terminal string. X is reachable if there is a derivation S ⇒* αXβ.

If grammar G' is obtained from G by removing all productions involving non-useful symbols, L(G') = L(G).

Algorithm

The first step is to identify the grammar's fruitful nonterminals: 

q := empty queue
F := ∅     // F is the set of nontermials known to be fruitful
do for each production A ——> α ∈ P  // P is the set of productions
|  if A ∉ F ∧ α ∈ Σ*    // Σ = set of terminal symbols
|  |  F := F ∪ {A}
|  |  q.enqueue(A)
|  fi
od

// At this point, all nonterminals that produce a terminal
// string in one step are in F and on the queue.  
// The following loop places into F all remaining fruitful nonterminals.

do while !q.isEmpty()
|  B := q.dequeue();   
|  do for each production A ——> αBβ   // in which B occurs 
|  |  if A ∉ F ∧ every nonterminal X in αβ satisfies X ∈ F 
|  |  |  F := F ∪ A
|  |  |  q.enqueue(A)
|  |  fi
|  od
od

Upon completion of the above, the set F contains all fruitful nonterminals. Eliminate from grammar G any production whose left-hand side is a non-fruitful nonterminal or whose right-hand side includes any non-fruitful nonterminal. Call the resulting grammar G1.

The second step is to identify the reachable nonterminals of G1 and to eliminate any productions involving non-reachable nonterminals. If S (the start symbol of G) is not among the fruitful nonterminals of G just computed, then L(G) = ∅ and we are finished. (Take G' to be the grammar with start symbol S and having no productions!)

Otherwise, construct a directed graph whose nodes are labeled by the nonterminals of G1. For nodes labeled A and B, place an edge going from A to B iff B occurs on the right-hand side of a production (in G1) whose left-hand side is A. (That is, (A,B) is an edge in the graph iff G1 has a production A → αBβ for some α and β.)

Now perform a search in the directed graph (e.g., breadth-first using a queue or depth-first using a stack or recursion) to find which nodes are reachable from S (the node labeled by the start symbol of G1). To obtain G', remove from G1 every production involving a variable that is not reachable.

Example

We follow the algorithm described above to eliminate useless symbols from the following context-free grammar (having start symbol S), thereby obtaining an equivalent CFG all of whose symbols are useful.

S→aSa  |  bB  |  bAA   (1) (2) (3)
A→abb  |  SbA  |  aB   (4) (5) (6)
B→AB  |  CaB   (7) (8)
C→cC  |  Sa  |  bD   (9) (10) (11)
D→dD  |  λ   (12) (13)

Solution: First we identify fruitful nonterminal symbols, i.e., those from which at least one terminal string can be derived.

Productions (4) and (13) imply that A and D, respectively, can produce a terminal string in one step. Hence, at the conclusion of the first loop in the algorithm, both A and D will be members of F and on the queue.

Iterations of the second loop correspond to the following analysis.

All the nonterminals on the right-hand side of Production (3) (namely, A) are fruitful, and thus its left-hand side (S) is fruitful. Similarly, Production (11) implies that C is fruitful. The remaining nonterminal is B, but none of its productions has a right-hand side composed entirely of known-to-be-fruitful symbols. (Indeed, each such right-hand side contains B itself.) Thus, we conclude that B is the lone non-fruitful nonterminal symbol and we eliminate all productions involving it. That leaves us with the grammar

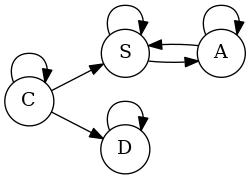
S→aSa  |  bAA   (1) (2)
A→abb  |  SbA   (3) (4)
C→cC  |  Sa  |  bD   (5) (6) (7)
D→dD  |  λ   (8) (9)

Next we identify the nonterminals that are "reachable" from the start symbol, S, and eliminate all productions involving unreachable nonterminals. To do this, draw a directed graph whose nodes correspond to the nonterminals and in which an edge from node X to node Y corresponds to there being a production in the grammar whose left-hand side is X and whose right-hand side includes an occurrence of Y. The nodes reachable by paths from node S correspond to the reachable nonterminals.

For our small grammar, it was hardly necessary to explicitly build the graph, because it is obvious that the only nonterminal reachable from S, other than itself, is A. Thus, nonterminals C and D are unreachable and we can eliminate all productions in which they play a part. The resulting grammar is

S→aSa  |  bAA   (1) (2)
A→abb  |  SbA   (3) (4)